The center and radius of an inscribed circle in a triangle
The center of a circle inscribed in a triangle is the intersection point of the bisectors of this triangle. The radius of a circle inscribed in any triangle is equal to twice the area of the triangle divided by its perimeter.
.The center and radius of the inscribed circle in the triangle through the coordinates of its vertices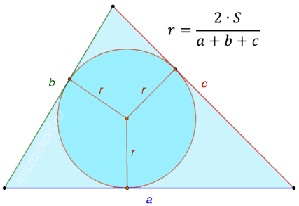
The coordinates of the vertices of the triangle and the known coordinates of the point are known. It is necessary to establish that the point belongs to the triangle.
There are several ways to determine. does the point lie inside the triangle or outside:
1. The method of comparing areas – according to Heron’s formula, there are areas of 3 triangles that form a point with each side of the triangle, then the area of the triangle itself is found and compared with the sum of the 3 previous triangles, if the sums are equal, then the point belongs to the triangle.
2. The relativity method – the orientation of movement along the vertices of the triangle is selected, for example clockwise. According to this orientation, we pass all the sides of the triangle, considering them as straight lines, and calculate on which side of the current straight line our point lies. If a point for all straight lines lies on the right side, which means that the point belongs to a triangle, if at least for some straight line it lies on the left side, then the membership condition is not fulfilled.
3. The geometric ray method – a ray is launched from a point along any axis in any direction. The number of intersections with the sides is calculated, if the number is odd, then the point lies inside the polygon.