Centre et rayon du cercle inscrit dans le triangle
Le centre du cercle inscrit dans le triangle est le point d’intersection de la bissectrice de ce triangle. Le rayon d’un cercle inscrit dans un triangle est égal au double de la surface du triangle divisée par son périmètre.
.Le centre et le rayon du cercle inscrit dans le triangle à travers les coordonnées de ses sommets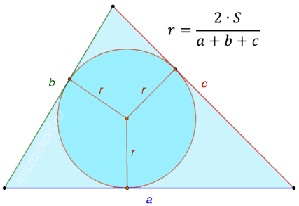
Les coordonnées des sommets du triangle et les coordonnées connues du point sont connues. Vous devez définir l’appartenance du point au triangle.
Il existe plusieurs façons de déterminer. est-ce que le point est à l’intérieur du triangle ou à l’extérieur:
1. La méthode de comparaison des zones-selon la formule de Geron sont les zones des triangles 3 qui forment un point de chaque côté du triangle, puis il y a la zone du triangle lui-même et est comparé à la somme des triangles 3 précédents, si les sommes sont égales, alors le point appartient au triangle.
2. Méthode de relativité-sélectionne l’orientation du mouvement sur les sommets du triangle, par exemple dans le sens des aiguilles d’une montre. Selon cette orientation, nous passons tous les côtés du triangle, en les considérant comme des droites, et nous calculons de quel côté de la droite actuelle se trouve notre point. Si le point pour toutes les lignes est sur le côté droit, alors le point appartient au triangle, si au moins pour une ligne, il se trouve sur le côté gauche, alors la condition d’appartenance n’est pas remplie.
3. Méthode du faisceau géométrique – à partir d’un point, un faisceau est lancé le long d’un axe dans une direction quelconque. Le nombre d’intersections avec les côtés est calculé, si le nombre est impair, alors le point se trouve à l’intérieur du polygone.