Mittelpunkt und Radius des eingeschriebenen Kreises in einem Dreieck
Der Mittelpunkt des in das Dreieck eingeschriebenen Kreises ist der Schnittpunkt des Bisektrises dieses Dreiecks. Der Radius eines Kreises, der in ein beliebiges Dreieck eingeschrieben ist, entspricht der doppelten Fläche eines Dreiecks, geteilt durch seinen Umfang.
.Der Mittelpunkt und der Radius des eingeschriebenen Kreises in ein Dreieck durch die Koordinaten seiner Scheitelpunkte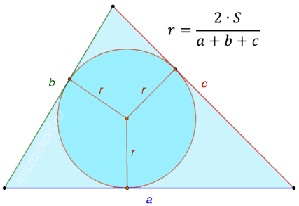
Die Koordinaten der Eckpunkte des Dreiecks und die bekannten Koordinaten des Punktes sind bekannt. Sie müssen die Zugehörigkeit des Punktes zum Dreieck festlegen.
Es gibt mehrere Möglichkeiten zu definieren. liegt der Punkt innerhalb des Dreiecks oder außerhalb:
1. Methode zum Vergleich von Flächen – nach der Geron-Formel gibt es Flächen von drei Dreiecken, die einen Punkt mit jeder Seite des Dreiecks bilden, dann ist die Fläche des Dreiecks selbst und wird mit der Summe der drei vorherigen Dreiecke verglichen, wenn die Summe gleich ist, dann gehört der Punkt zum Dreieck.
2. Relativitätsmethode – Wählen Sie die Ausrichtung der Bewegung an den Ecken eines Dreiecks aus, z. B. im Uhrzeigersinn.In dieser Ausrichtung passieren wir alle Seiten des Dreiecks, betrachten sie als gerade, und wir berechnen, auf welcher Seite der aktuellen Geraden unser Punkt liegt. Wenn der Punkt für alle Geraden auf der rechten Seite liegt, dann gehört der Punkt zum Dreieck, wenn er zumindest für eine Gerade auf der linken Seite liegt, dann wird die Zugehörigkeitsbedingung nicht erfüllt.
3. Methode des geometrischen Strahls – Ein Strahl wird von einem Punkt aus auf einer beliebigen Achse in eine beliebige Richtung ausgelöst. Die Anzahl der Schnittpunkte mit den Seiten wird berechnet, wenn die Anzahl ungerade ist, dann liegt der Punkt innerhalb des Polygons.