Distance between a point and a plane
The distance from a point to a plane is the distance from a point to a point where one of them is given, and the other is on the plane and is a projection on a given plane. To build a projection on a plane, it is necessary to lower the perpendicular to the plane.
.The distance between a point and a plane knowing the coordinates of the point and the equation of the plane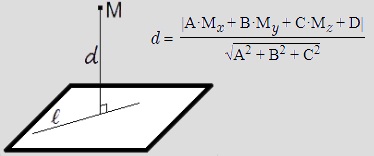
Enter the coordinates of the point M:
x1 =
y1 =
z1 =
Enter the equation of the plane:
*X +
*Y -
*Z -
= 0
d=
Examples of solving problems using a calculator
Example #1: find the distance between the plane 2x + 5y – 6z – 7 = 0 and the point M(1, 3, 6).
Ответ: the distance from the point to the plane is 7.44.
Example #2: find the distance between the plane 3x + 6y – 8z – 9 = 0 and the point M(2, 5, 8).
Answer: the distance from the point to the plane is 10.44.