Distance entre un point et un plan
La distance d’un point à un plan est la distance d’un point à un point où l’un est donné et l’autre est sur le plan et est une projection sur un plan donné. Pour construire une projection sur un plan, vous devez abaisser la perpendiculaire sur le plan.
.Distance entre le point et le plan connaissant les coordonnées du point et l’équation du plan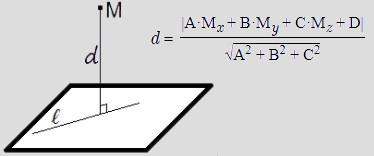
Entrez les coordonnées du point M:
x1 =
y1 =
z1 =
Entrez l'équation du plan:
*X +
*Y -
*Z -
= 0
d=
Exemples de résolution de problèmes à l’aide d’une calculatrice
Exemple №1: trouver la distance entre le plan 2x + 5y-6z-7 = 0 et le pointM(1, 3, 6).
Réponse: la distance entre le point et le plan est égale à 7.44.
Exemple №2: trouver la distance entre le plan 3x + 6y-8z – 9 = 0 et le point M(2, 5, 8).
Réponse: la distance entre le point et le plan est égale à 10.44.