Ellipsen-Quadrat-Rechner
Eine Ellipse ist eine geschlossene Kurve auf einer Ebene, die als Schnittpunkt einer Ebene und eines Kreiszylinders oder als orthogonale Projektion eines Kreises auf eine Ebene erhalten werden kann. Ein Kreis ist ein Sonderfall einer Ellipse. Um die Fläche der Ellipse zu kennen, müssen wir die Länge der beiden Halbachsen oder die Länge der beiden Achsen der Ellipse kennen. Wenn Sie die angegebenen Werte kennen, können wir die Formel verwenden, um die Fläche der Ellipse zu berechnen.
.Die Fläche der Ellipse entlang der Länge der beiden Halbachsen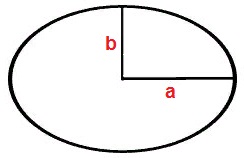
Die Fläche der Ellipse entlang der Länge der beiden Achsen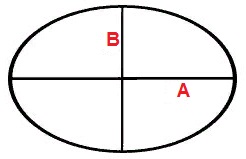
Formel für die Berechnung der Fläche S – auf Halbachsen a, b: S= πab
Formel zur Berechnung der S-Fläche an Achsen A, B: S= πAB/4
Wobei S die Fläche ist, a und b die Halbachse, A und B die Achse der Ellipse sind, π ist die Zahl Pi, die immer ungefähr 3,14 ist.