The volume of the ball sector
To find the volume of the spherical sector, it is enough to remember one simple formula that includes two unknown parameters (if we count together with pi– three). But first, let’s remember what each word of the designated concept describes.
.The volume of the ball sector
Formulas and definitions
Volume (from lat. volume–”filling”) is a quantitative characteristic of the space occupied by a body or substance.
A ball (i.e., a geometric body) is a collection of all points of space that are located in it from the center at a certain distance (read. in a certain distance; it is also considered its radius), which appears to be no more than the value set for it.
The sector here denotes a certain “limitation” in the space of the corresponding form.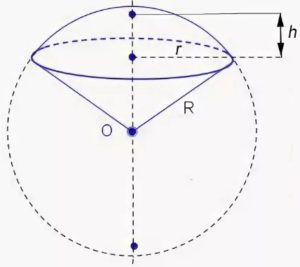
In other words, it is a part of the [volume] of the ball (it also appears to be a kind of geometric body), which is bounded by the curved surface of the spherical segment (not to be confused with the spherical segment) and a conical surface with a base and vertex in the form of the base of the segment and the center of the ball, respectively.
Two formulas for calculating the volume of the ball sector:

where h – is the height of the ball segment that belongs to the ball sector,
R– radius of the [large circle] ball;
the number π is a mathematical constant equal to 3.14.