Odległość między punktem a płaszczyzną
Odległość od punktu do płaszczyzny To odległości od punktu do punktu, w którym jeden z nich jest dany, a drugi znajduje się na płaszczyźnie i jest rzutowany na daną płaszczyznę. Aby zbudować rzut na płaszczyznę, konieczne jest obniżenie prostopadłego do płaszczyzny.
.Odległość między punktem a płaszczyzną znając współrzędne punktu i równanie płaszczyzny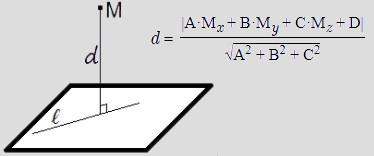
Wprowadź współrzędne punktu M:
x1 =
y1 =
z1 =
Wprowadź równanie płaszczyzny:
*X +
*Y -
*Z -
= 0
d=
Przykłady rozwiązywania problemów za pomocą kalkulatora
Przykład №1: znajdź odległość między płaszczyzną 2x + 5y-6z-7 = 0 a punktem M(1, 3, 6).
Odpowiedź: odległość od punktu do płaszczyzny wynosi 7.44.
Przykład №2: znajdź odległość między płaszczyzną 3x + 6y – 8z-9 = 0 a punktem M(2, 5, 8).
Ответ: odległość od punktu do płaszczyzny wynosi 10.44.